Energy Analysis of Long Integer Algorithms
During the summer of 2022, I completed an REU (Research Experience for Undergraduates) internship at IUPUI. I worked in a research group, in the Department of Electrical and Computer Engineering, that focused on profiling the energy consumption of large integer arithmetic algorithms. Cryptographic signature authentication on wireless sensor networks was the application of the research. By the end of the internship, I nearly finished an entire library that supported modular exponentiation for RSA and scalar point multiplication on elliptic curves over prime and binary fields.
Research Background
While execution time remains one of the most researched areas of algorithmic and software optimization, with numerous resources existing on the subject, energy consumption is a far less studied but equally important topic in applications such as wireless sensor networks (WSN). A company or government might wish to collect data for an AI program using sensor nodes that are placed in remote locations. To prevent malicious attacks such as data poisoning, devices should implement an authentication protocol for messages that are sent on the network. Signature verification will be hindered by the energy constraints of each node. The goal of the research project was to analyze how various optimizations affected the energy consumption of ECDSA and RSA on the ESP32 platform.
Our group (mostly me) wrote a library in C/C++ that implemented all the underlying algorithms needed to perform modular exponentiation and scalar point multiplication. We stored numbers using arrays of unsigned long integers. The number was represented using a base 232 numeral system, so each element in the array was a coeffecient of some power of 232. We started by writing a bitwise 32-bit multiplication algorithm and then used it to write a schoolbook multiplication algorithm for our 32-bit array data type. We also implemented schoolbook addition, bit-shifting, rounding, and other utility algorithms. Those served as the foundation for a long division algorithm that returned both a quotient and remainder. From there, modular exponentiation was implemented using the square and multiply method (a.k.a. binary exponentiation). An algorithm to compute the modular multiplicative inverse of a number was also implemented using the Extended Euclidean algorithm.
Various optimization algorithms were then discussed and implemented. We implemented a squaring algorithm, Karatsuba's trick, Chinese remainder theorem, and windowing using the m-ary method which is just an extension of binary exponetiation. One strange occurrence was the performance of our optimization using Chinese remainder theorem; we saw, approximately, a 2.83X speed-up instead of the theoretical 4X speed-up in runtime. The unit test sample size was small and the theoretical speed-up calculuation relies on assumptions about time complexity and algorithmic input size, so it is possible our result is reasonable.
We then started implementing data structures and arithmetic for elliptic curves. We made a point addition and point doubling algorithm and used them to construct scalar point multiplication. The point operations and curve data came from NIST standards. We used curves of the Weierstrass form. The scalar point multiplication algorithm bore a striking resemblance to the modular exponentiation algorithm. In fact, the code was nearly identical; the main difference was that the squares were replaced with doubles and the multiplications were replaced with adds. We also optimized the operations by relying on Mersenne prime fields and Solinas' method for fast modular reduction on those primes.
The energy analysis was performed using a current clamp and oscilloscope. Originally, we tested our algorithms on a Windows PC. We placed the probes around clusters of wires going to the CPU and RAM modules. Then, we would capture the current signal on a USB drive connected to an oscilloscope. We also kept track of the supply voltages for the modules using a mulitmeter. During data analysis, we would multiply the current signal by the module's respective supply voltage to obtain the power. Performing numerical integration on the power signal over the duration of program execution yielded the energy consumption. We also computed the static power consumption using the data outside of the current spike. Our uncertainty quantification took into account uncertainty in the start and stop time, quantization error, and deficiencies in the numerical integration process.
We found there was a lot of noise in the signals we measured from the PC. Our executables were forced to run in an operating system environment; background processes and magnetic interference from other modules degrade the data, even if you run the PC in safe mode without a GUI. There was also an issue with Windows choking the program execution if CPU usage reached a certain threshold. To improve the data quality, I duplicated the library and altered it so that it could run on an ESP32 microcontroller. That allowed us to avoid OS complications and to factor in smaller sources of error such as the energy consumption from LEDs on the MCU.
Image Gallery
 Placement of Current Probes on RAM and CPU
Placement of Current Probes on RAM and CPU
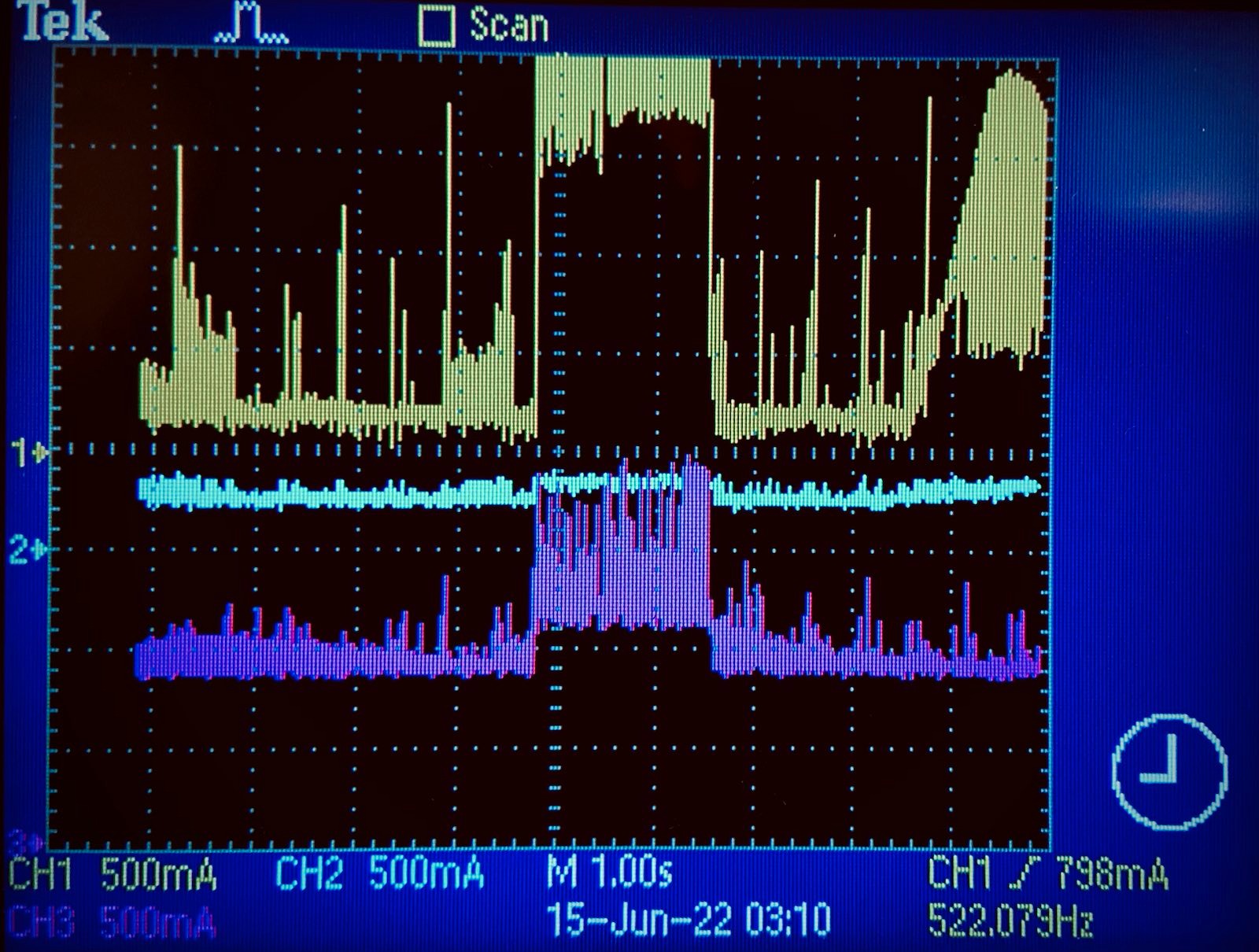 Current Spike from Program Execution
Current Spike from Program Execution
 Measurement Setup for Running Executables on PC
Measurement Setup for Running Executables on PC