Radiation Analysis of Microprocessors in Space
I am currently assisting with research in the Reliable Electronics and Systems Lab at the Luddy School of Informatics, Computing, and Engineering. The lab analyzes the effect of ionizing radiation on microelectronics in space. My research centers around the security concerns of total ionizing dose degradation of symmetric key infrastructures on microprocessors. We are targeting the MSP430FR6989 mixed-signal microcontroller, which sees frequent use in CubeSat missions and has a cryptographic acceleration/generation module.
Research Background
The Consultative Committee for Space Data Systems (CCSDS) has developed a recommended standard on cryptographic algorithms and an informational report on key management systems that should be used on all missions by CCSDS member agencies. Protection of information should occur between many end points of a space mission including the communication link between the spacecraft and a ground station. The telemetry downlink contains sensitive telemetry and science data while the telecommand uplink contains sensitive reconfiguration and application-specific commands. The spacecraft must be able to encrypt and decrypt these payloads in a fast and efficient manner to ensure mission success. Symmetric-key algorithms provide the same security level as public-key algorithms while using less memory for key storage and while executing in substantially faster time frames, especially within hardware implementations. For that reason, symmetric-key hardware accelerators are present on many system-on-chip (SoC) devices.
Ionizing radiation can hinder the spacecraft's symmetric key infrastructure by not only degrading the accuracy of its cryptographic accelerator but also by changing the entropy of its random bit generator (RBG). Any symmetric key infrastructure usually employs a hierarchy of symmetric keys. A master key is stored in read-only memory for emergency cases while keys for encrypting other keys and ensuring traffic protection are frequently generated and recycled. If the key generation facility of the spacecraft is compromised, then new keys can not be securely generated which requires emergency use of the master key. Use of one key for many purposes and with no clearly defined cryptoperiod is a known security risk for secret key retrieval using cryptanalysis.
Total ionizing dose (TID) data has been collected for many internal SoC modules of commercial SoC microprocessors, such as the ADC, SRAM, and clock system modules. In spite of the importance of encrypted communication links, few analyses have been brought forth on the TID performance of cryptographic modules in complex SoC devices. While the MSP430FR6989 chip and other related models in the MSP430x5xx and MSP430x6xx family have been tested in radiation environments before, the research has generally focused on obtaining pass/fail data of internal modules under increasing doses of ionizing radiation. No data, pass/fail or otherwise, to the best of our knowledge, has been presented on the cryptographic acceleration and generation module of this family.
The implementation of a symmetric-key infrastructure on a spacecraft that uses this family of microcontrollers requires knowledge of (1) when the AES accelerator will fail to correctly encrypt or decrypt payloads and (2) when the chosen key generation facility will fail to produce random bit sequences. The threshold that indicates when the AES coprocessor fails will be found by irradiating the device under test with an increasing dose until the coprocessor produces incorrect results. For analysis of RBG reliability, the randomness of a collection of true and pseudo-RBG techniques will be compared under an increasing dose. The randomness will be compared by applying two standard batteries: the NIST SP 800-22 Suite and the NIST SP 800-90B Suite. SP 800-22 is a collection of null hypothesis tests that analyze the distribution of the output of random number generators. SP 800-90B is a collection of statistical estimators that measure the min-entropy of the generator source.
Min-entropy is a more conservative estimate of randomness than Shannon entropy, and it is defined as
for a discrete variable with distribution Ω.
The radiation test is currently on track to be performed in January. The results will be submitted to a conference by February.
WILL BE UPDATED WITH MORE INFORMATION AS THE PROJECT PROGRESSES
Image Gallery
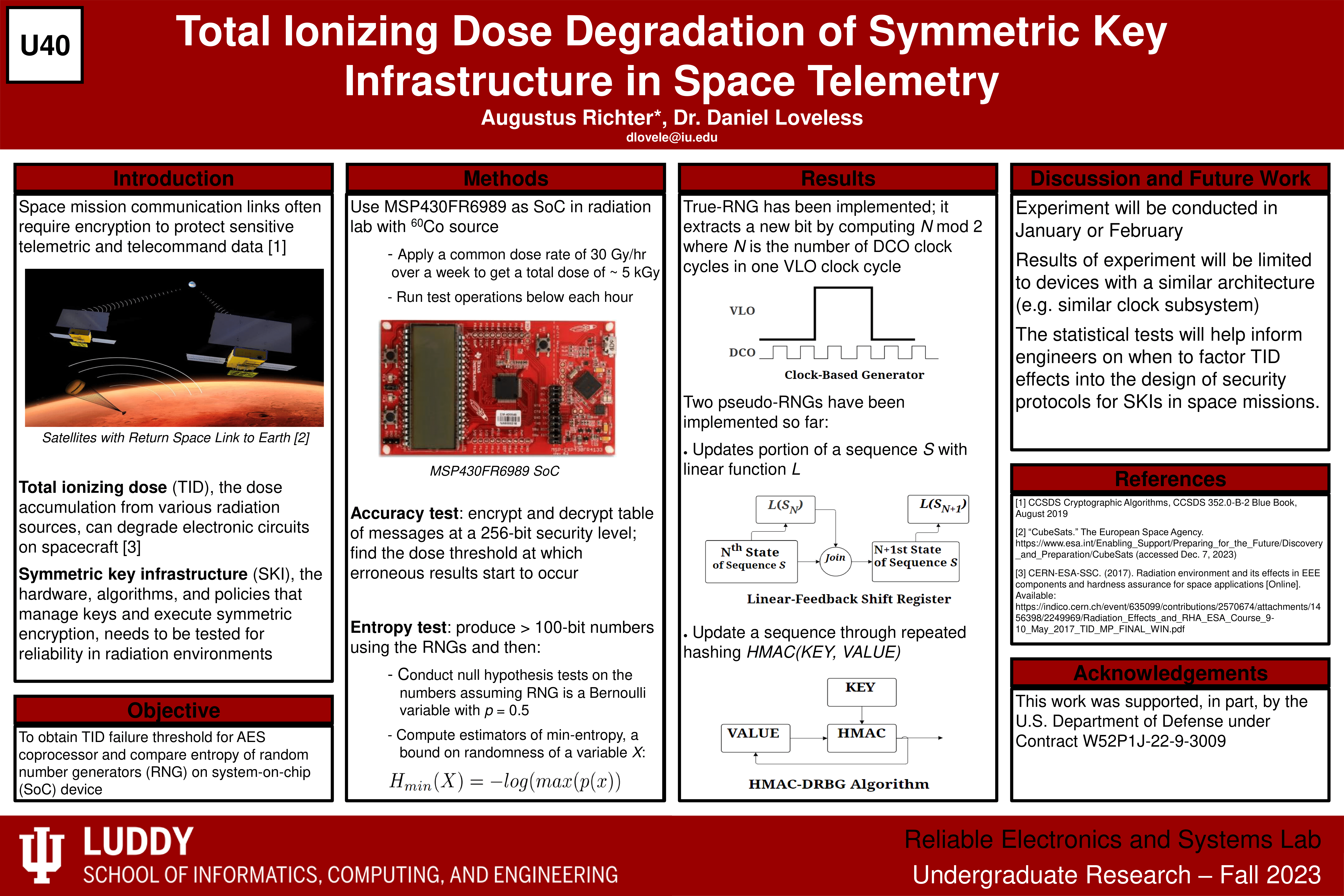 Poster on Current Progress of Research for the Luddy UROC Fall 2023 Poster Session
Poster on Current Progress of Research for the Luddy UROC Fall 2023 Poster Session
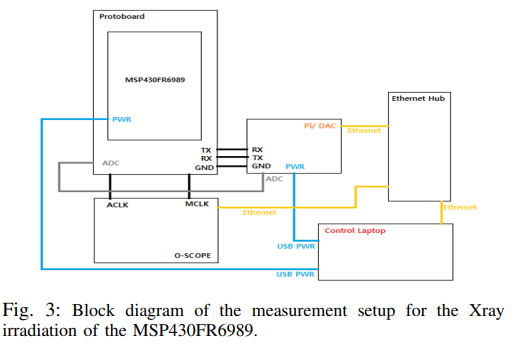 Similar Test Setup for a Different RES Lab Experiment that Estimated Dose Based on Clock Signals
Similar Test Setup for a Different RES Lab Experiment that Estimated Dose Based on Clock Signals